Las ecuaciones estructurales son una herramienta estadística fundamental en la investigación médica, utilizada para analizar relaciones complejas entre variables observadas y latentes. Este método permite a los investigadores estimar múltiples ecuaciones interrelacionadas de manera simultánea, lo que resulta especialmente útil para evaluar modelos teóricos que proponen caminos causales entre diferentes factores. Por ejemplo, se puede estudiar cómo la inflamación y la disfunción de órganos afectan los resultados de los pacientes, como los costos y la mortalidad en unidades de cuidados intensivos.
Además, las ecuaciones estructurales permiten modelar constructos latentes, que son variables no observables definidas por indicadores observables. Esto incluye aspectos como la salud percibida o la calidad de vida relacionada con la salud. Al admitir diversos tipos de datos y combinaciones de modelos, las ecuaciones estructurales se han convertido en una herramienta versátil en la investigación médica, ayudando a desentrañar la complejidad de las relaciones en el ámbito de la salud.
Información más importante:
- Las ecuaciones estructurales permiten analizar relaciones complejas entre variables en la investigación médica.
- Facilitan la estimación simultánea de múltiples ecuaciones interrelacionadas, considerando errores de medición.
- Son útiles para probar modelos teóricos que relacionan variables como inflamación y disfunción orgánica con resultados de pacientes.
- Permiten modelar constructos latentes, como la salud percibida, a través de indicadores observables.
- Admiten diversos tipos de datos, incluyendo resultados continuos y binarios, lo que las hace versátiles.
Ecuaciones estructurales: fundamentos y su importancia en medicina
Las ecuaciones estructurales son un marco estadístico potente utilizado en la investigación médica para analizar las relaciones complejas entre variables observadas y latentes. Este enfoque permite a los investigadores estimar múltiples ecuaciones interrelacionadas de forma simultánea, lo que resulta crucial para comprender cómo diferentes factores pueden influir en la salud de los pacientes. Al abordar la medición de errores, las ecuaciones estructurales ofrecen una visión más precisa de las dinámicas subyacentes en los datos médicos.
La importancia de las ecuaciones estructurales en medicina radica en su capacidad para probar modelos teóricos que postulan caminos causales. Por ejemplo, pueden ayudar a investigar cómo la inflamación y la disfunción orgánica afectan los resultados de los pacientes, como la mortalidad y los costos en unidades de cuidados intensivos. Esto permite a los investigadores no solo analizar datos, sino también formular hipótesis que pueden guiar futuros estudios y tratamientos en el ámbito de la salud.
Comprendiendo el modelo de ecuaciones estructurales en salud
El modelo de ecuaciones estructurales (SEM) se basa en la idea de que las relaciones entre variables pueden ser representadas de manera matemática. En el contexto de la salud, el SEM permite a los investigadores modelar constructos latentes, que son variables no observables definidas a través de indicadores observables. Por ejemplo, la calidad de vida relacionada con la salud puede ser evaluada a partir de respuestas a cuestionarios que miden diferentes aspectos de la salud.
Los componentes del SEM incluyen variables observadas, que son los datos que se recopilan directamente, y variables latentes, que son inferidas a partir de las observaciones. Este enfoque ayuda a descomponer la complejidad de los datos médicos y a identificar relaciones causales entre diferentes factores, proporcionando una visión más clara de cómo interactúan las variables en la salud de los pacientes.
Ventajas de usar ecuaciones estructurales en investigaciones médicas
El uso de ecuaciones estructurales en investigaciones médicas ofrece múltiples ventajas que mejoran la calidad y la precisión de los análisis. Una de las principales ventajas es su capacidad para manejar relaciones complejas entre variables, lo que permite a los investigadores obtener una comprensión más profunda de cómo diversos factores interactúan en el ámbito de la salud. Además, el modelo de ecuaciones estructurales facilita la identificación de relaciones causales, lo que es fundamental para el desarrollo de teorías y tratamientos en medicina.
Otro beneficio significativo es que SEM permite la inclusión de variables latentes, lo que ayuda a capturar aspectos no observables de la salud, como la calidad de vida o la percepción de salud. Esto proporciona una visión más completa y precisa de los datos, lo que puede llevar a mejores decisiones clínicas y políticas de salud pública.
- Identificación de relaciones causales: Permite establecer conexiones directas entre variables que afectan la salud.
- Modelado de variables latentes: Facilita la evaluación de constructos no observables, enriqueciendo el análisis.
- Simultaneidad en la estimación: Posibilita la evaluación de múltiples ecuaciones interrelacionadas de forma simultánea.
- Reducción de errores de medición: Mejora la precisión de los resultados al considerar errores sistemáticos.
- Versatilidad en el análisis de datos: Admite diferentes tipos de datos, lo que la hace aplicable en diversas investigaciones.
Aplicaciones prácticas de ecuaciones estructurales en estudios clínicos
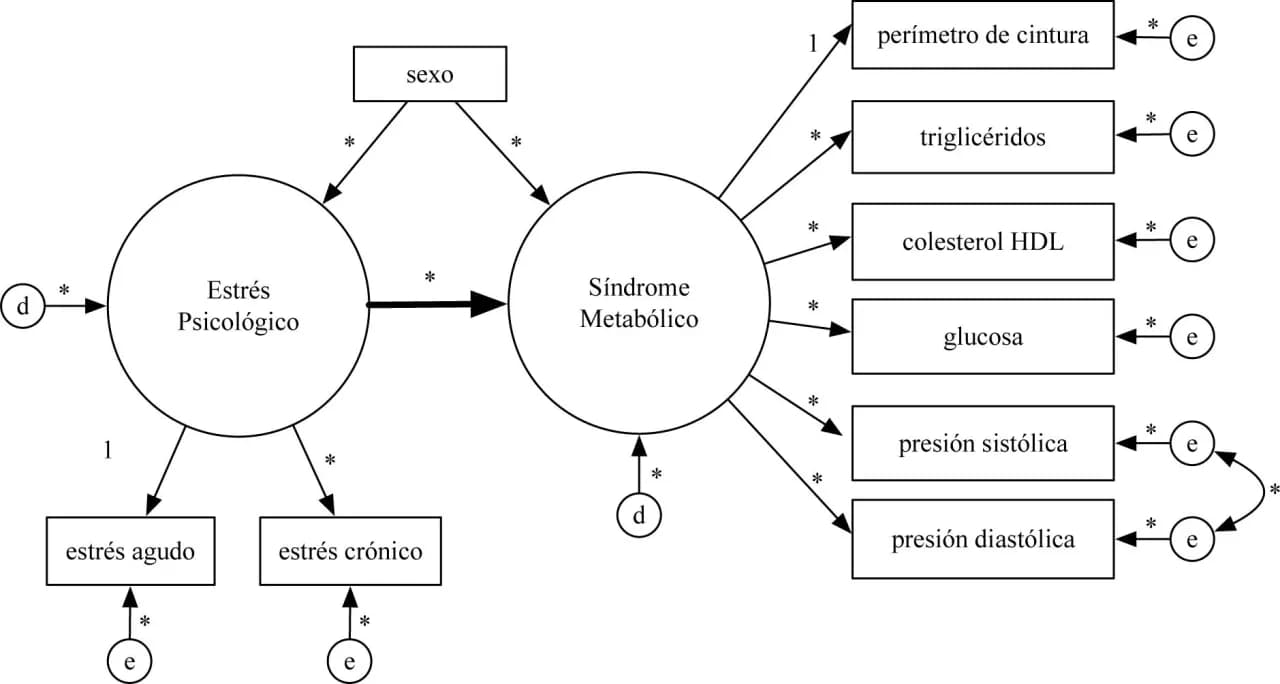
Las aplicaciones de ecuaciones estructurales en investigación médica son numerosas y variadas, lo que demuestra su relevancia en la práctica clínica. Estas aplicaciones permiten a los investigadores analizar datos complejos y extraer conclusiones significativas que pueden influir en la atención médica y la salud pública. Por ejemplo, en estudios sobre la relación entre el estrés y la salud mental, el SEM puede ayudar a identificar cómo diferentes factores contribuyen a los trastornos psicológicos.
Además, el uso de modelos de ecuaciones estructurales ha sido fundamental en investigaciones sobre el impacto de tratamientos específicos en la calidad de vida de los pacientes. Un estudio reciente demostró que la intervención temprana en pacientes con enfermedades crónicas mejora significativamente su percepción de salud y bienestar. Este tipo de análisis es crucial para diseñar estrategias efectivas de intervención y mejorar los resultados en salud.
Ejemplos de estudios médicos que utilizan SEM para análisis
Un estudio notable que utilizó modelos de ecuaciones estructurales es el realizado por la Universidad de Salud Pública de Barcelona, donde se investigó la relación entre el estilo de vida, la salud mental y la calidad de vida en adultos mayores. Los investigadores aplicaron SEM para analizar cómo factores como la actividad física, la dieta y el apoyo social influyen en la salud mental y, a su vez, cómo esto afecta la calidad de vida. Los resultados mostraron que un estilo de vida activo y el apoyo social positivo están estrechamente relacionados con mejores resultados en salud mental y calidad de vida.
Otro ejemplo es un estudio llevado a cabo en el Hospital Universitario de Copenhague, que exploró el impacto de la inflamación en pacientes con enfermedades crónicas. Utilizando ecuaciones estructurales en investigaciones médicas, los investigadores pudieron establecer conexiones entre marcadores inflamatorios, la función orgánica y los resultados clínicos. Este análisis ayudó a identificar que la inflamación no solo afecta directamente la salud física, sino que también tiene un impacto significativo en la calidad de vida de los pacientes.
Cómo SEM ayuda a identificar relaciones complejas en salud
El uso de modelos de ecuaciones estructurales (SEM) es fundamental para desentrañar las relaciones complejas entre variables en el ámbito de la salud. SEM permite a los investigadores modelar tanto variables observadas como latentes, lo que ofrece una comprensión más rica de cómo diferentes factores interactúan. Por ejemplo, al analizar la relación entre el estrés, la salud mental y la calidad de vida, SEM puede ayudar a identificar cómo el estrés influye en la salud mental, y a su vez, cómo esto impacta en la calidad de vida de los pacientes.
Además, SEM facilita la identificación de caminos causales, permitiendo a los investigadores probar hipótesis sobre la dirección y la naturaleza de las relaciones. Este enfoque es especialmente útil en estudios donde múltiples factores pueden influir en un resultado de salud, ya que proporciona un marco para evaluar simultáneamente estas interacciones. Así, SEM se convierte en una herramienta poderosa para el análisis de datos complejos en la investigación médica.
Leer más: Investigaciones clínicas de dispositivos médicos: normas y procesos esenciales
Retos y limitaciones en la implementación de SEM en medicina
La implementación de modelos de ecuaciones estructurales (SEM) en el ámbito médico presenta varios desafíos significativos. Uno de los principales retos es la necesidad de contar con grandes volúmenes de datos de alta calidad, ya que SEM es sensible a la cantidad y la calidad de las observaciones. Además, la complejidad de los modelos puede dificultar la interpretación de los resultados, especialmente si los investigadores no tienen experiencia previa con esta metodología. Otro desafío es la adecuada especificación del modelo, ya que un modelo mal especificado puede llevar a conclusiones erróneas sobre las relaciones entre variables.
Las limitaciones de SEM también son relevantes en el contexto de la investigación médica. Por ejemplo, aunque SEM puede manejar relaciones complejas, no puede establecer causalidad de manera definitiva sin un diseño experimental adecuado. Además, la dependencia de supuestos como la normalidad de los datos y la linealidad puede limitar su aplicabilidad en ciertos contextos clínicos. Finalmente, la interpretación de los constructos latentes puede ser subjetiva, lo que introduce un nivel de incertidumbre en los resultados que debe ser considerado al realizar análisis en salud.
Desafíos comunes al aplicar ecuaciones estructurales en investigación
Al aplicar ecuaciones estructurales en investigaciones médicas, los investigadores enfrentan varios desafíos comunes. Uno de los más significativos es la necesidad de un tamaño de muestra adecuado, ya que un número insuficiente de participantes puede afectar la estabilidad y la validez de los resultados. Además, la complejidad de los modelos puede llevar a problemas de convergencia, donde el modelo no logra encontrar una solución adecuada. También es común que los investigadores se enfrenten a dificultades en la identificación de variables latentes, especialmente si estas no están bien definidas en la literatura existente. Por último, la falta de formación específica en SEM entre los investigadores puede resultar en una aplicación incorrecta de la metodología, lo que puede comprometer la calidad de los hallazgos.
Estrategias para superar obstáculos en el uso de SEM
Para abordar los desafíos en la implementación de modelos de ecuaciones estructurales (SEM) en investigaciones médicas, es crucial adoptar estrategias efectivas. Primero, se recomienda realizar una capacitación adecuada para los investigadores en el uso de SEM, lo que incluye cursos y talleres que expliquen tanto la teoría como la práctica. Además, es fundamental asegurar que se disponga de un tamaño de muestra adecuado para mejorar la robustez de los resultados. También se sugiere utilizar software estadístico especializado que facilite la modelización y análisis de datos, permitiendo una mejor visualización y comprensión de los resultados. Por último, fomentar la colaboración entre equipos multidisciplinarios puede enriquecer el análisis y proporcionar diferentes perspectivas que ayuden a superar las limitaciones inherentes al uso de SEM.
| Desafíos | Estrategias para superarlos |
|---|---|
| Tamaño de muestra insuficiente | Asegurar un tamaño de muestra adecuado mediante planificación y diseño de estudios |
| Complejidad del modelo | Capacitación en SEM para investigadores y uso de software especializado |
| Identificación de variables latentes | Colaboración con expertos en el tema para definir claramente los constructos |
| Problemas de convergencia | Revisar la especificación del modelo y realizar ajustes según sea necesario |
Integración de SEM con tecnologías emergentes en medicina
La combinación de modelos de ecuaciones estructurales (SEM) con tecnologías emergentes, como la inteligencia artificial (IA) y el aprendizaje automático, está abriendo nuevas posibilidades en la investigación médica. Estas tecnologías pueden ayudar a manejar grandes volúmenes de datos y a identificar patrones complejos que pueden no ser evidentes a simple vista. Por ejemplo, al integrar SEM con algoritmos de aprendizaje profundo, los investigadores pueden optimizar la identificación de variables latentes y mejorar la precisión de los modelos, lo que resulta en análisis más robustos y significativos.
Además, la implementación de plataformas de big data en el ámbito de la salud permite a los investigadores acceder a una cantidad masiva de datos clínicos y de pacientes, facilitando el uso de SEM para analizar relaciones complejas en tiempo real. Esto no solo mejora la calidad de la investigación, sino que también permite la personalización de tratamientos y estrategias de intervención basadas en los perfiles individuales de los pacientes. A medida que estas tecnologías continúan evolucionando, se espera que el uso de SEM se convierta en una herramienta aún más poderosa para avanzar en la medicina personalizada y en la comprensión de la salud poblacional.